人生の見方が変わる統計用語６選

僕にとって統計を勉強する醍醐味は何と言っても日々の意思決定やキャリアに統計的考え方が生きる、というところでしょう。この醍醐味を少しでも多くの人に味わってもらうべく、統計のコンセプトと、それが人生にどう役立つかの事例をご紹介します。一部機械学習やコンピューターサイエンス、数学の考え方も混ぜてみました。

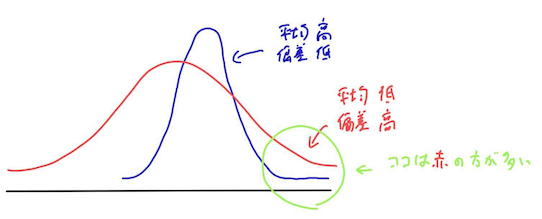
1. 平均と偏差 (mean and variance)

「A社とB社、どっちに就職しようかな。。A社は平均は低いかもだけど偏差が高いからちゃんと部署を選べばめっちゃ成長できるかも！」

平均の意味は皆さんご存知かと思います。偏差は偏差値に代表されるように、データのばらつき具合を言います。 例えば、学校を選ぶとき、周りの学生が優秀かどうかは大事な指標になるかと思いますが、平均的な能力値だけではなく、能力値の偏差（ばらつき）も見るべきです。なぜなら、学生の中で自分が関わることになるのは一握りであることを考えると、偏差が大きければ大きいほど質の高い学生コミュニティーを見つけられる可能性が高くなるからです。 よくアメリカの大学生の理数能力が日本の大学生のそれと比較されることがありますが、僕は前者は平均が低く偏差が大きいとみています。現に、今関わっている友達は理数能力がえぐいほど高いので、上位10%くらいのコミュニティーに属せているのかな、と思います。あくまで感覚値ですが。

能力値のような上下がはっきりしているもの以外でも、偏差が大きい環境の方が自分の居場所を見つけやすくなるのではないでしょうか。

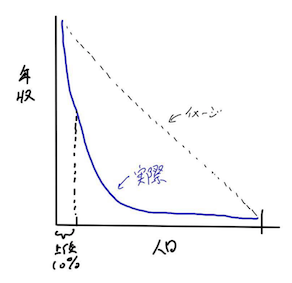
2. ジップの法則 (Zipf’s Law)

「勤めあげたら年収１０００万までは行けるかもしれないけど、指数関数的な収入の増加は望めないな。。どうすれば非線形に収入を増やせるか考えてみよう！」

上位８人の富豪が下位５０％と同等の資産を持っているというニュースをみたことがあるでしょうか。もちろんいつの時代もこのように格差がここまでひどい訳ではないでしょうが、このようなごく限られた人々への富の集中はいつの時代も起こってきました。それは収入の分布が上位にいけば行くほど指数関数的に増えて行くからです。このような指数関数的関係をジップの法則(Zipf’s Law)と言います。これは富の格差に限らずありとあらゆるところに出現します。例えば本に出てくる単語の頻出度合いはジップの法則に従います。つまり、最頻出する単語、例えば、てにをは、私、僕、などの言葉は、他の単語よりも圧倒的に多く登場するのです。他にもTwitterのフォロワー数、FacebookのLike数や、企業の社員数など、ありとあらゆるものがジップの法則に従います。

僕らは学校教育のせいか物事が線形に増加すると思いがちです。だから、例えば富が一部の上位層に集中していることを知った時に、必要以上に憤りを覚えてしまうかもしれません。これを基にして考えれば、自分のキャリアに関して、線形的な自己成長が自分を他人より優位に立たせることは少ないかも、と考えることができます。年収１０００万から１億は額の差は多けれど人口比の差はそれほど大きくない。ということはこのままちまちま勤め上げる、というようなことをしても他人と比較した場合には同じポジションにとどまり続ける、ということになります。もちろん、それを気にするかどうかというのは別問題ですが、言いたいのはジップの法則を線形的な増加と同じくらい自然な分だと感覚的に理解することができれば、いろんなものが見えてくるのではないかということです。

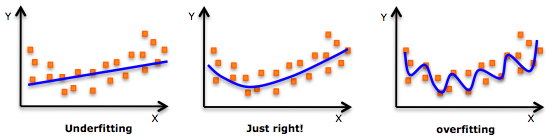
3. 過学習 (overfitting)

「テスト勉強しまくったのに点取れない。。あ、過学習してるかも！」

勉強をしていて、練習問題はスラスラ解けるけど、本番で少し違うパターンの問題が出たらうまく解けな買った、という場合には過学習を疑う必要があります。過学習とは与えられたデータに対してモデルを当てはめ過ぎてしまうことによって、新たに与えられたデータに対してそのモデルが有用じゃなくなってしまうことを言います。

大学受験は無敵だったのに会社に入ったらうまく仕事をこなすことができない、日本でうまくいった企業が海外でうまくいかない、テニス部でペアを替えたらすごく弱くなってしまった、ある女の子をメロメロにさせた方法が他の子には全然通用しない。このような場合には自分が培ってきたスキルがこれまでの経験に過学習している場合があります。

こういった場合、統計ではモデルを正則化（データに過敏に反応しないようにすること）したり、学習するデータを増やしたりします。人生でも同様に、何か経験から学ぶときは汎用的になるように気をつけ、学ぶ際になるべく多種多様な経験をする方向に自分を向かわせてみるべきでしょう。

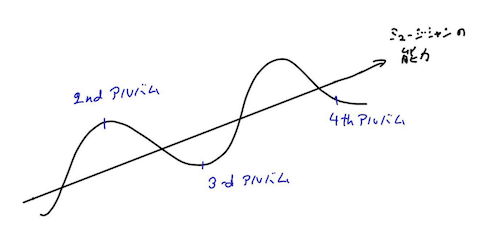
4. 平均への回帰 (regression to the mean)

「今回のサザンのアルバムイマイチだったけど、平均へ回帰してるのかな。もうしばらくファンでいよう」

大好きだったアーティストの新しいアルバムが期待外れだった、という経験はないでしょうか。一流大学に通っていた友達Aくんのその後の人生が思っていたより輝かしいものでなかった、という経験はないでしょうか。これは好きなアーティストやAくんの能力が下がってきた、というだけではないことがあります。一般的に観測するデータにはノイズが含まれます。このノイズはランダムであり、ある時には結果をよくするようなノイズが含まれ、ある時には結果を悪くするノイズが含まれます。例えば、最初にアーティストに出会ったアルバム（2ndアルバムとしましょう）は、彼らの能力を実際よりも高く見せようとするプラスのノイズが足されていたのかもしれません。その場合、仮に彼らの能力がその後伸びていたとしても、3rdアルバムは彼らの能力にマイナスのノイズが足されていた、ということがありえます。このような現象を統計では平均への回帰と言います。

よくできた親の子供には期待をかけがちだったり、株の売買がうまくいったときは今後もうまくいく、などと思いがちですが、これは平均への回帰に逆行する考え方です。平均への回帰を念頭に置くことでよりスマートな期待値コントロールができるでしょう。

5. 探索と活用 (exploration and exploitation)

「大学生はまだ人生の中では探索のフェーズだ。活用しようと焦らずに色々試してみよう」

これはコンピューターサイエンスの中の一分野、強化学習の用語です。強化学習とは自動運転や将棋ソフトなどの背景にある技術で、人工知能に色々なパターンを試させることでどんどん人工知能を成長させて（強化させて）いきます。一般的には、最初の方は探索(Exploration)といって、例えば将棋ならいろんな手を試してみて勝敗の確率がどの程度かをとにかく学びまくります。だんだん人工知能が成長してくると、活用(Exploitation)といって、これまで学んだ手の中で勝ちやすい手を中心に勝負していきます。

自分の脳を人工知能と考えて、経験から学んでいくプロセスを強化学習と考えれば、私たちの意思決定にも探索と活用のような考え方が大事になってくることがわかるでしょう。どのタイミングで一般教養を磨くところから専門性を磨くところにスイッチするのか、具体的に言えば、例えば大学は専門学校に行くべきか普通科の大学に行くべきか、これを探索と活用のフレームワークに落とし込むと綺麗に整理することができます。より強化学習を学べば、探索と活用のトレードオフについて、より熟慮した上で自分の人生の意思決定ができるのではないでしょうか。

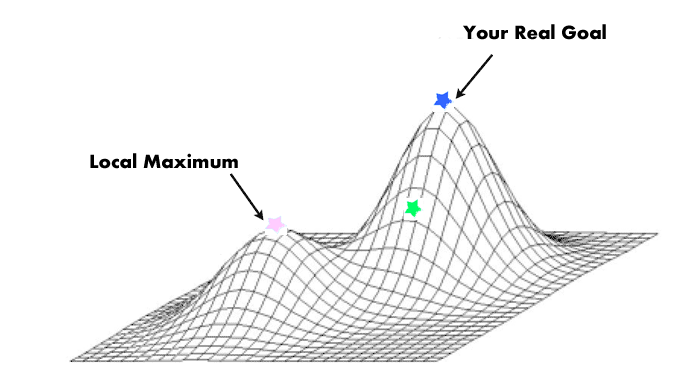
6. 全体最適と極所最適 (local optima and global optima)

「最近営業の成績が伸び悩んでるな。局所最適にハマってるのかもしれないから、全く新しいやり方も試しみようかな」

これは絵を見たら一発でわかると思います。以下のLocal Optimaが局所最適です。小さい丘の上に登っても、大きい丘にそのまま登ることはできません。一旦低いところに降りて、また大きい丘に向かって登って行く必要があります。これは、現状の改善を続けて行くだけでは必ずしも物事の最適解には行き着かない、ということを示しています。時には斬新な方法を試みて見る必要があります。この考え方は数理最適化の分野に登場します。

例えば仕事の効率が前より上がっていかなくなった、カップルの仲があまり深まらなくなった、ABテストでウェブサービスを改善しても前ほどKPIの上昇が見られない、こういった場合には全体最適を目指して勇気を持って今立っている小さい丘を下ってみましょう。

他、因果関係と相関関係、セレクションバイアス、再現率と適合率、無定義語など、物事を考える際に度々持ち出している用語はたくさんありますが、今回はこの辺で。みなさんの人生が統計によって少しでもいいものになりますように！